반응형
What is Rotation Matrix?
The rotation Matrix refers to the dynamic change of the angle of the vector without affecting the length or magnitude. Normally, the coordinates of the vector are defined by (x, y).
x = R.cos(α), y = R.sin(α)

After rotating the matrix at any new angle, we can define x and y as:
x = R.cos(α + β)
y = R.sin(α + β)
with the help of the formula,
cos(α + β) = cos(α)cos(β) - sin(α)sin(β)
sin(α + β) = cos(α)sin(β) + sin(α)cos(β)
we can define new coordinates of a vector with:
x1 = R.cos(α)cos(β) - R.sin(α)sin(β)
y1 = R.cos(α)sin(β) + R.sin(α)cos(β)
and then we can replace R.cos(α) with x and R.sin(α) with y
x1 = x.cos(β) - y.sin(β)
y1 = x.sin(β) + y.cos(β)
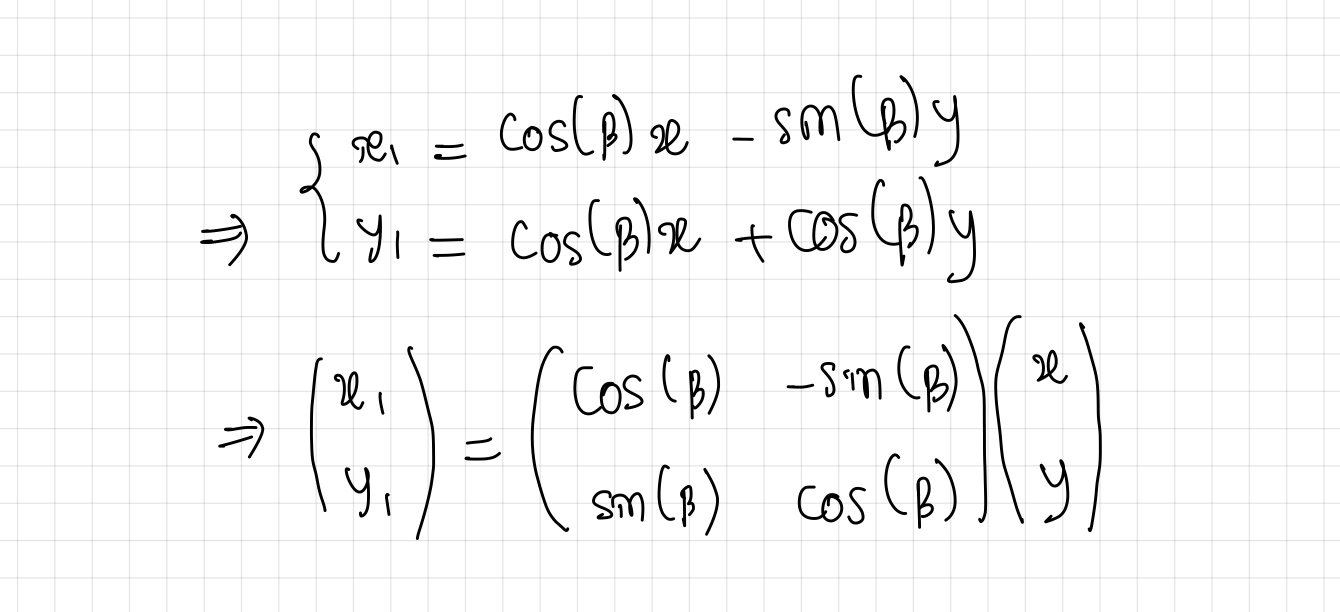
반응형
'Mathematics > Linear Algrebra' 카테고리의 다른 글
| Hermitian Matrix in Linear Algebra (0) | 2023.08.05 |
|---|---|
| Polar coordinates in 2D (0) | 2023.08.05 |

