Linear Regression with Python

Table of Contents

• Linear Regression
  • What is Linear Regression?
  • When do we use Linear Regression?
• Python 
  
  • Packages for Linear Regression
  • Simple Linear Regression

Linear Regression

What is Linear Regression?

Linear regression is a mathematical algorithm which is commonly used for data analysis.  In Linear Regression, there are two types of variable ( dependent variable &  independent variables ). 

 

Mock Dataset

Age	Gender	Genre
20	One	HipHop
23	0	Classsical
25	0	Jazz
26	One	Jazz

According to this data, age and gender are classified as independent variables and genre is an dependent variable.

Python

Package for Linear Regression

 # required libraries 
 import numpy as np
   import pandas as pd
   import matplotlib.pyplot as plt

Pandas is a Python library used for working with data sets and Matplotlib is a library used for visualization.

 

Dataset: https://www.kaggle.com/datasets/peterkmutua/student-hours-scores

 # get data from local 
 data = pd.read_csv( 'score.csv' )
 
 
 # plotting actual data points 
 plt.scatter(hours, scores, color= "m" , marker= "o" , s= 30 )
 plt.show()

result: 

 

Finding coefficient

def   find_coefficient  (x, y) :
    observation_count = np.size(x)
    mean_of_x = np. mean
    mean_of_y = np. mean

    # calculating cross-deviation and deviation about x
    SS_xy = np.sum(y * x) - observation_count * mean_of_y * mean_of_x
    SS_xx = np.sum(x * x) - observation_count * mean_of_x * mean_of_x

    # calculating regression coefficients
    b_1 = SS_xy / SS_xx
    b_0 = mean_of_y - b_1 * mean_of_x

    return b_0, b_1

Full Code

import numpy as np
  import matplotlib.pyplot as plt
  import pandas as pd


def   find_coefficient  (x, y) :
    observation_count = np.size(x)
    mean_of_x = np.mean(x)
    mean_of_y = np. mean(y)

    # calculating cross-deviation and deviation about x
    SS_xy = np.sum(y * x) - observation_count * mean_of_y * mean_of_x
    SS_xx = np.sum(x * x) - observation_count * mean_of_x * mean_of_x

    # calculating regression coefficients
    b_1 = SS_xy / SS_xx
    b_0 = mean_of_y - b_1 * mean_of_x

    return b_0, b_1


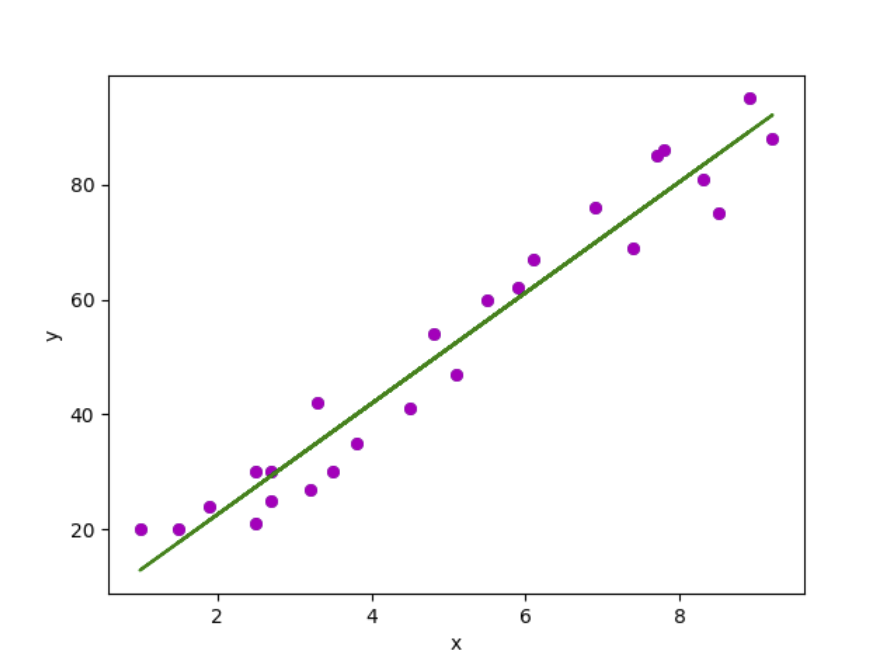
def   plot_regression_line  (x, y, b) :  
    # plotting the actual points as scatter plot 
    plt. scatter(x, y, color= "m" ,
                marker= "o" , s= 30 )

    # predicted response vector 
    y_pred = b[ 0 ] + b[ 1 ] * x

    # plotting the regression line 
    plt.plot(x, y_pred, color= "g" )

    # putting labels 
    plt. xlabel( 'x' )
    plt.ylabel( 'y' )

    # function to show plot
    plt.show()


def   main  () :  
    data = pd.read_csv( 'score.csv' )
    hours = data[ 'hours' ]
    scores = data[ 'score' ]

    co_efficient = find_coefficient(hours, scores)
    plot_regression_line(hours, scores, co_efficient)


if __name__ == "__main__" :
    main()

 

Result: